Introduction: Some biological attributes of organisms scale proportionately with body size; for a given type of organism the relationship between a physical or physiological attribute and body size is the same regardless of the organism's size. Often, however, this relationship changes relative to the size of the organism. For example, metabolic rate increases with body mass, but increases less than one would expect if the relationship were simply proportional. On the other hand, skeleton weight increases with body mass more than expected based on simple proportionality. Similar relationships are found in plants: tree diameter increases with height, but at a greater-than-proportional rate. These are examples of allometric relationships, in which the scaling relationship between some biological attribute and body size is dependent on the organism's size.
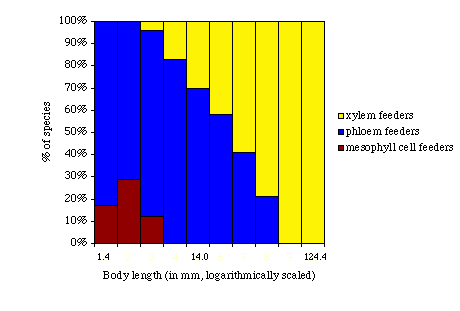
The distribution of species with different feeding modes among body size classes is shown below for the herbivorous insect fauna of India (graph redrawn from Novotny & Wilson, 1997 [data from Distant, 1906-18, in Novotny & Wilson]). For each body size class (indexed by body length) the graph shows the percentage of species in that size class that feed on xylem, phloem, or mesophyll cells.

Importance: A change in size, whether during the course of an organism's lifetime or the course of a taxon's evolution, imposes physical and physiological constraints. In the case of a skeleton or a tree trunk, for example, an increase in size would be constrained by problems of strength if not compensated for by changes in allometric relationships.
Question: Can allometric relationships explain the lack of small xylem-feeding insect species?
Variables:
| Y | a biological variable, such as body mass or length |
| a | constant in allometric equations |
| b | constant in allometric equations |
| Bv | body volume (mm3) |
| Xv | volume flow of xylem fluid (m3/s) |
| P | suction pressure gradient (Pa or MPa) |
| c | length of food canal (m) |
| r | radius of food canal (m) |
| L | cibarial pump load (s-1) |
| Fv | frontoclypeus volume (mm3) |
Methods: A biological variable is often expressed by an allometric scaling equation of the form:
![]()
where Y can be any biological variable (such as metabolic rates or cross-sectional areas of tree trunks), a is a constant called the proportionality coefficient, b is the scaling exponent (which is equal to the slope of the line of the equation when plotted on logarithmic coordinates), and the last term often is some index of organism size such as body volume (Bv in this case) or body mass (M). A well-known allometric equation relates metabolic rate to body mass: Y = aM 3/4. The value of the proportionality coefficient (a) depends on the kind of organism.
The body size distributions of xylem-sucking insects (Auchenorrhyncha, Hemiptera) indicate that xylem feeders tend to be larger than either phloem or mesophyll cell feeders. The feeding structures in these insects (food canal and cibarial pump) change more or less in equal proportion (isometrically) with body volume, rather than allometrically (Novotny & Wilson, 1997). However, metabolic rate is known to be relatively higher in smaller animals. Novotny and Wilson hypothesize that, given the low nutrient content of xylem and the increase in suction pressures needed to extract it as feeding apparatus size decreases, there is an allometric change in the energetic costs of xylem feeding. In other words, there is a relatively higher energetic cost for smaller animals because a) they have to expend relatively more energy extracting xylem due to the size of their feeding structures, and b) they have to extract relatively more xylem because of their high metabolic rates. This leads to an allometric equation:
![]()
in which the volume flow of xylem fluid (Xv) is assumed to be proportional to metabolic rate (i.e., the percentage of energy from xylem that becomes available to the insect is independent of body size). The authors then derived the following equation to describe the allometric relationship between the suction pressure gradient (P) necessary to cause a given volume flow through the food canal and body volume (Bv):
![]()
where P is the pressure gradient (measured in Pascals [Pa]), aP is a constant, Bv is body volume (in mm3), c is the length of the food canal (in m), and r is the radius of the food canal (in m). This relationship indicates that smaller species must generate relatively higher pressures to draw xylem fluid into the feeding canal.
The authors also used cibarial pump load to quantify energetic costs associated with feeding. The cibarium is the preoral cavity formed by the mouthparts; in sucking insects it is often modified to form a pump. The muscle volume of this pump, which is directly proportional to the work generated by muscle contraction, was approximated by the frontoclypeus volume, Fv (mm3). The ratio between the volume flow of xylem fluid (Xv) and the frontoclypeus volume is the cibarial pump load:
![]()
We can see from this equation that for a given volume flow of xylem fluid (Xv), cibarial pump load (L) increases as frontoclypeus volume (Fv) decreases. For smaller species, then, the cibarial pump load is higher.
The graph below shows the relationships between the log10 of body volume (in mm3) and sucking pressure, P, on the left axis (in megapascal or MPa) and cibarial pump load, L, on the right axis (L is given as a per-second (s-1) value, since it is a ratio with units [mm3/s]/[mm3]). (Graph redrawn from Novotny & Wilson, 1997).
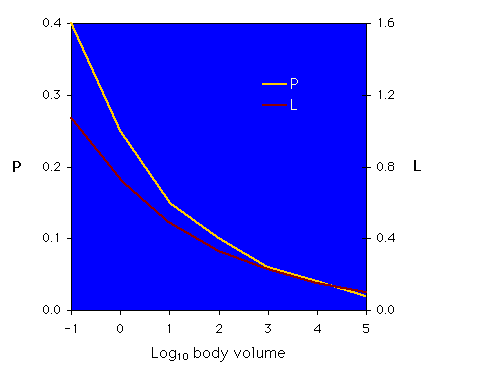
The regression equations for the two lines are P= 0.25Bv-0.21 and L = 0.73Bv-0.17.
Interpretation: The P and L allometries presented by the authors indicate that there is an advantage to being larger in size. The graph of the regression for P (yellow line) shows a decrease in the sucking pressure needed to extract xylem fluid as body volume increases; the graph of L (red line) shows a similar decrease in cibarial pump load with increasing body volume. There does indeed appear to be an allometric change in the energetic costs associated with xylem feeding.
Conclusions: The first graph (body length by percent of species) shows that among the fauna examined there are no small xylem feeding species. Novotny and Wilson demonstrate that the energetic cost of extracting sufficient quantities of xylem fluid is relatively higher as body size decreases; i.e., the allometric relationships between body volume and P and L lead to an allometric change in the energetic costs imposed by feeding on xylem. The authors suggest that energetic costs may constrain the evolution of smaller body sizes in this group of insects.
Additional Questions:
1) What are some of the advantages of larger body size? What would some advantages to smaller body size be?
2) What would the graphs of body volume x P or body volume x L look like if you graphed them on a log-log plot? How would you interpret these graphs?
Sources: Nobel, P. S. 1983. Biophysical Plant Physiology and Ecology. W. H. Freeman, San Francisco, CA.
Novotny, V. and M. R. Wilson. 1997. Why are there no small species among xylem-sucking insects? Evolutionary Ecology 11:419-437.
Romoser, W. S. and J. G. Stoffolano, Jr. 1994. The Science of Entomology, 3rd ed. Wm. C. Brown Publishers, Dubuque, IA.
Schmidt-Nielson, K. 1984. Scaling: Why is Animal Size So Important? Cambridge University Press, New York, NY.
copyright 1999 by M. Beals, L. Gross, and S. Harrell