Introduction: Messenger RNA is transcribed as a complementary copy of DNA that will eventually be translated into an amino acid chain. mRNA travels from the nucleus to the cytoplasm for translation. Because mRNA is constantly being degraded in the cytoplasm, it is synthesized at a much higher rate than necessary for maintenance of a steady amount.

Importance: Measuring the half-life of mRNA is difficult to determine experimentally because it is so short lived. However, knowledge of the half-life of mRNA can provide information about the stability of different types of mRNA. For example, in the 1970's, the discovery that the 3` end of mRNA molecules contained a poly A tail (a 200 nucleotide sequence) raised questions about its function. We can use equations describing the decay of mRNA and the growth of cells to estimate the half life of mRNA.

Questions: Can we estimate the half-life of mRNA? Does knowledge of mRNA half-life give information about the poly A tail?

Methods: Experimentally, one can measure the amount of mRNA in an exponentially growing cell population. Amount of mRNA present initially is measured by labelling. As the cells in the culture continually double, the cell population and the total amount of mRNA grow exponentially. Meanwhile, the initially labelled mRNA is decaying exponentially at some rate determined by its half-life. The ratio of remaining labelled mRNA to total mRNA in the growing cell population is monitored over time and graphed.

Total mRNA (M) can be considered to grow exponentially over time at a rate determined by the cell growth rate (K) and the initial amount of mRNA (M₀):

It is convenient to write the growth rate (K) in terms of the doubling time of the cell population. We take M₀ = 1, M = 2, and t = D (doubling time) and then solve for K. We find K = ln2 / D. By substituting this into the original equation, we get

Similarly, the amount of labelled mRNA (L) initially present can be considered to decay exponentially at a rate determined by the mRNA half life (H):

The total amount of mRNA accumulation combines the equations determining the accumulation of mRNA as the cell population grows and the decay of mRNA as determined by its half life.

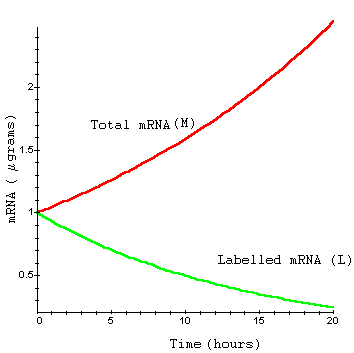
The ratio of originally labelled mRNA to total accumulating mRNA is given by L/M. Therefore the ratio of unlabelled mRNA to total mRNA is given by 1- L/M. As the originally labelled mRNA decays, this ratio will eventually go to 1. This ratio is given by

This equation can be fitted to experimental data. The half-life (H) can then be estimated from the graph. For example, we can collect and graph data on the accumulation of mRNA with a poly A tail and Histone mRNA, which lacks a poly A tail, in order to compare the two. By fitting the above equation to the data, when K is known, we can determine which value of H gives the best fit for the data. H is then an estimate of the mRNA half life.

Interpretation: Looking at the graphs the different mRNAs, we can see that for Histone mRNA, the fraction of unlabelled mRNA goes to 1 very quickly. This implies that the originally labelled Histone mRNA decays much more quickly than poly A mRNA.

Greenberg (1972) calculated the half-life for mRNA containing poly A tails using this method and graphs similar to those above. He had previously determined the doubling time of the cell population (D) to be 15 hours. He then determined which value of H resulted in the best fit of (1 - L/M) to the data. He determined the half-life (H) for poly A mRNA to be 10 hours. Half-lives for Histone mRNA, which lacks a poly A tail, or mRNA in the presence of a poly A inhibitor were considerably lower (30 minutes).

Conclusion: The turnover of mRNA lacking a poly A tail is much higher than mRNA containing a poly A tail. Poly A may play a role in translation of mRNA by increasing the stability of mRNA and allowing mRNA to function normally. Exponential equations and graphs make it easier for the half-lives of mRNA to be calculated and compared.

1. Work through the algebra to write the function 1-L/M from the functions L and M.

2. Examine the graph of the functions L and M. Determine how the doubling time and half-life affect the exponential growth or decay by plotting these graphs with different values of D and H.

3. You should know how to look at a graph of two functions and estimate the graph of a new function created when one function is divided by another. Estimate 1-L/M for a few values by looking at the individual graphs of L and M from Question 2.

Sources: Darnell, J., H. Lodish, and D. Baltimore. 1986. Molecular Cell Biology. Scientific American Books, Inc., New York

Greenberg, J. R. 1972. High stability of messenger RNA in growing cultured cells. Nature 240:102-104

Copyright 1999 M. Beals, L. Gross, S. Harrell